Sampling diverse NeurIPS papers using Determinantal Point Process (DPP)
It is NeurIPS time! This is the time of the year where NeurIPS (or NIPS) papers are out, abstracts are approved and developers and researchers got crazy with breadth and depth of papers available to read (and hopefully to reproduce/implement). Every person have a different approach to skim papers and discover new stuff. One approach is to pick one specific area of interest (natural language processing, computer vision, bayesian inference, optimization, etc), and go deep into a subject. Or one can go random and select at chance some papers to explore, and then exploit papers in the preferred domain. We will present a different approach here, where we will be able to select papers by diversity, meaning that we are willing to select papers that tend not to overlap and be equally distributed to each other. To do so, the idea here is to use determinantal point processes (DPPs) as a way to capture more diverse samples in a given sampling space. For a more detailed reading on DPPs, please consider reading the awesome paper Determinantal point processes for machine learning 1. A point process \(\mathcal{P}\) on a discrete set \(\mathcal{Y}\) is a probability measure on \(2^\mathcal{Y}\), all the possible subsets of \(\mathcal{Y}\). In a determinantal point process, a random subset Y will have, for every subset \(\mathcal{A}\) contained in \(\mathcal{Y}\) (\(\mathcal{A} \subseteq \mathcal{Y}\)) :
\[\mathcal{P}(\mathcal{A} \subseteq \mathcal{Y}) = det(K_{A})\]\(K_{A}\equiv[K_{i,j}]_{i,j\in A}\) in equation above represents the marginal kernel to compute probabilities of points \(i,j\) of any subset \(\mathcal{A}\) to be included in Y. By using determinal rule, we can represent \(\mathcal{P}\) as:
\[\mathcal{P}(i \in Y) = K_{ii} \\ \mathcal{P}(i,j \in Y) = K_{ii}K_{jj}-K_{ij}K_{ji} \\ \mathcal{P}(i,j \in Y) = \mathcal{P}(i \in Y) \mathcal{P}(j \in Y)-K_{ij}^2\]The last term in equation above (\(K_{ij}^2\)) determines the (anti) correlations bewtweens pairs of elements, meaning the large values of \(K_{ij}\) (high correlation in points) will tend not do co-occur. This is the part in the DPP formulation that ensures that it will sample for diversity.
In this experiment, we will like to sample a specific number of papers k, so in this case we will be using k-DPP 2 instead of pure kDPP. k-DPP conditions DPP with cardinality k, and ends up being a mixture of elementary DPP, by given nonzero weight \(\lambda_{n}\) to elements with dimension k. We experimented the really nice python library \(DPPy\) by Guillaume Gautier (more details here 3 and here 4) to run the code below.
First things, all the code on this post can be found in this Colab notebook:
2018 NeurIPS diverse papers w/ DPPy
For this experiment, we used NeurIPS 2018 papers from this link, as the 2019 papers are not yet available at this page (making easier to get abstracts using tools such as BeautifulSoup). Once the 2019 papers are available I will add the Colab notebook here.
Getting papers Title and Abstract with BeautifulSoup
I used the awesome Python lib BeautifulSoup in order to extract the papers Title and Abstract from NeurIPS official page. The first job is to get all paper title URL, and then explore each paper link and extract the abstract by searching for the subtitle and abstract classes. This is the function to extract abstract from a given URL:
def get_title_abstract(url):
response = requests.get(url)
soup = BeautifulSoup(response.text, "html.parser")
title = soup.find(attrs={'class' : 'subtitle'})
abstract = soup.find(attrs={'class' : 'abstract'})
return title.get_text(), abstract.get_text()
And here extracting all 2018 papers Title and Abstract and embedding information into a Pandas DataFrame:
links_url = 'http://papers.nips.cc/book/advances-in-neural-information-processing-systems-31-2018'
response = requests.get(links_url)
soup = BeautifulSoup(response.text, "html.parser")
main_wrapper = soup.find(attrs={'class' : 'main wrapper clearfix'})
paper_urls = []
for a in main_wrapper.find_all('a', href=True):
if '/paper/' in str(a):
paper_urls.append("http://papers.nips.cc" + a['href'])
print("Total papers in 2018: {}".format(len(paper_urls)))
nips_2018 = {}
for i in tqdm_notebook(range(len(paper_urls))):
t, a = get_title_abstract(paper_urls[i])
nips_2018[i] = {"title":t, "abstract":a}
nips_2018_dataframe = pd.DataFrame.from_dict(nips_2018, orient='index')
Embedding text with BERT
Now that we have all the necessary information in a dataframe, we will use sentence embeddings, more specifically BERT embeddings 5, to convert text into a vector in a latent space. To make things easier, I used the nice lib Flair from Zalando Research, averaging the embeddings (output dimension is = 3072). As input for the BERT embedder, the title and abstract were concatenated and had stopwords removed (no stemming or lemmatization were applied).
from flair.embeddings import BertEmbeddings
bert_embedding = BertEmbeddings()
def get_bert_embedding(sent):
sentence = Sentence(sent)
bert_embedding.embed(sentence)
all_tensors = torch.zeros(bert_embedding.embedding_length)
for token in sentence:
all_tensors+=token.embedding
return all_tensors/len(sentence)
Paper diversity with DPPy
Now to the final and most exciting part, on how to select diverse papers. In order to compare diverse papers sampled with DPP, I selected the closest (nearest) papers by applying cosine similarity of a given random paper with the whole set of 1009 papers from 2018 NeurIPS conference. In order to plot those papers in 2D, I used TSNE from Scikit-Learn 7 (with perplexity = 5).
The distribution of the closest (nearest) papers given a random selected paper is shown in the figure below. As we can see, most of the papers cluster together in the top right corner of the picture, confirming that they are similar when projecting the embeddings into 2D plane:
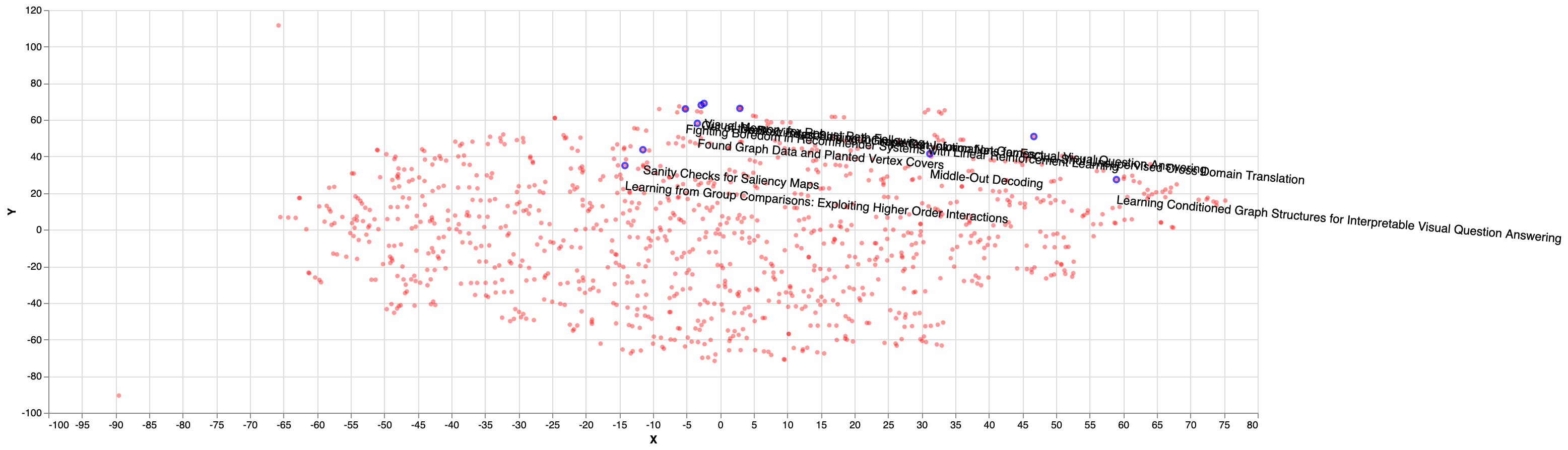
As for the random sampled papers, we can see on the figure below that they seem to be cluttered in some parts of the plane (bottom right) and not equally distributed:
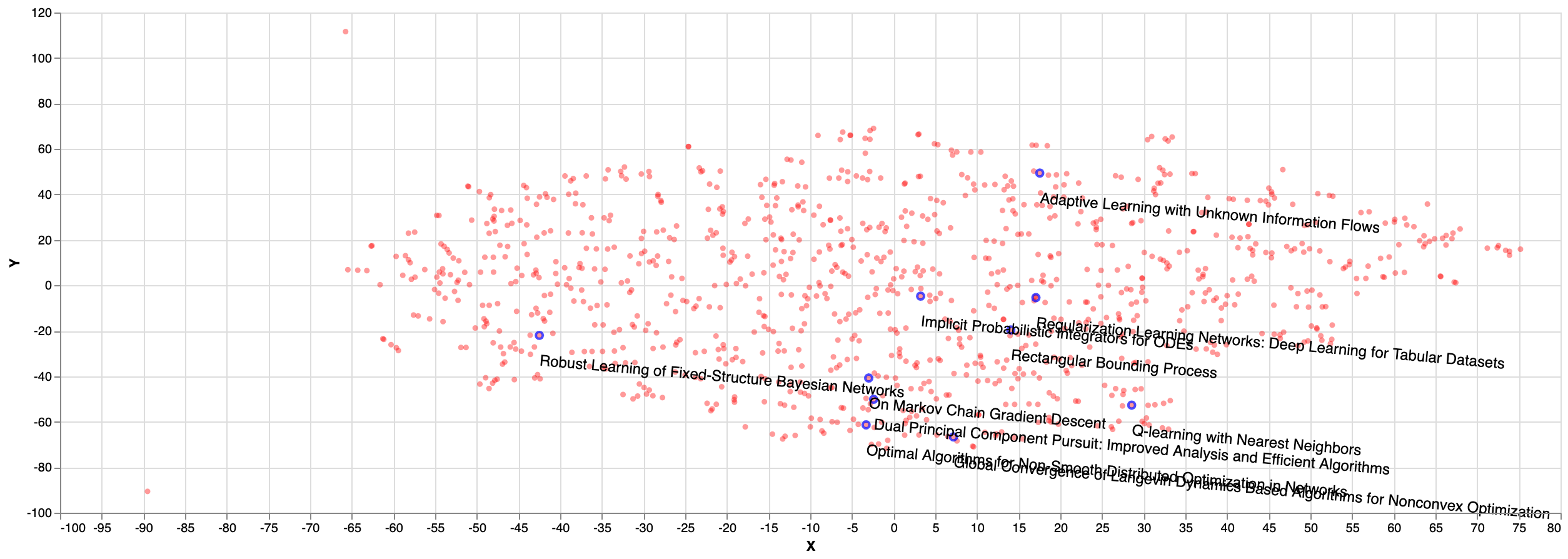
Finally, the figure below show papers sampled using k-DPP from DPPy library, with k size of 10 and likelihood kernel. As we can see, the distribution seem to be more diverse and more distributed in space than the previous methods (nearest, random):
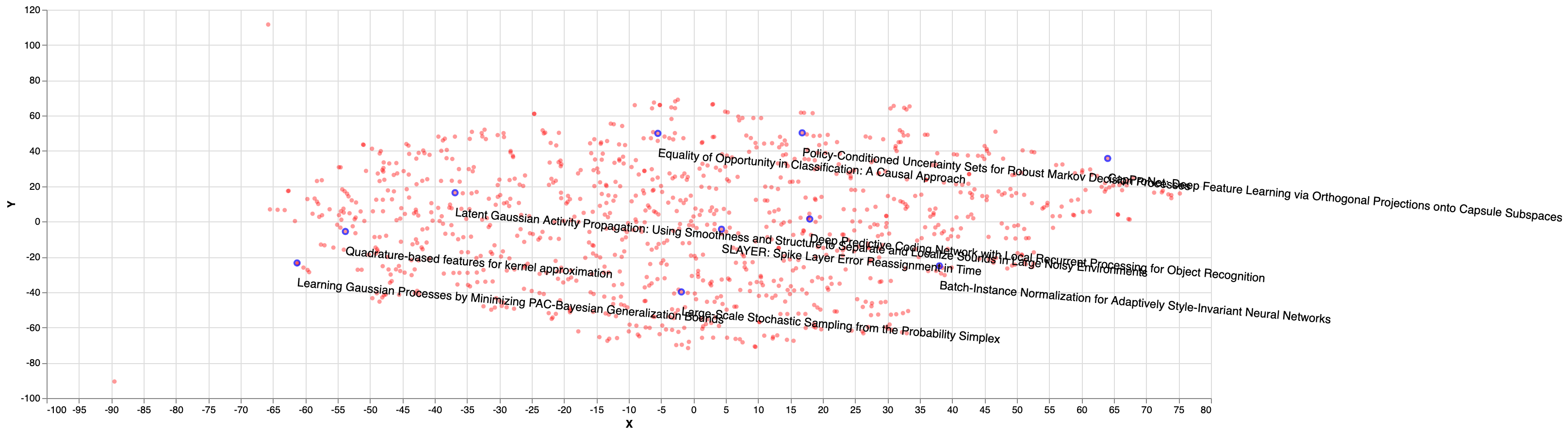
Finally, in order to compare these three sets in a more quantitative way, I measured average Jaccard similarity, cosine similarity and euclidean distance of nearest , random and diverse sets. It is interesting to note that, as the diverse set is more equally distributed in space, it’s Jaccard and Cosine similarity are lower, and the average Euclidean distance of the set is higher than the nearest and the random sets.
JACCARD SIMILARITY ---
RANDOM: 0.05260996952409507
DIVERSE: 0.04059503829222504
NEAREST: 0.04299341079777443
COSINE SIMILARITY ---
RANDOM: 0.9287719594107734
DIVERSE: 0.9257738563749526
NEAREST: 0.9476157267888387
EUCLIDEAN DISTANCES ---
RANDOM: 9.385317516326904
DIVERSE: 10.03541965484619
NEAREST: 8.910124270121257
Hope you enjoyed this post and find some nice applications for sampling with DPPs!
References
- Determinantal point processes for machine learning PDF
Alex Kulesza and Ben Taskar, 2012 - k-DPPs: Fixed-Size Determinantal Point Processes PDF
Alex Kulesza and Ben Taskar, 2011 - DPPy: Sampling DPPs with Python PDF
Guillaume Gautier, Guillermo Polito, Rémi Bardenet and Michal Valko, 2018 , 2018 - Python library for sampling Determinantal Point Processes Link
Guillaume Gautier, Guillermo Polito, Rémi Bardenet and Michal Valko, 2018 - BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding PDF
Jacob Devlin and Ming-Wei Chang and Kenton Lee and Kristina Toutanova, 2018 - Flair - A very simple framework for state-of-the-art Natural Language Processing (NLP) Link
Zalando Research - scikit-learn - Machine Learning in Python Link


